Algorithms Series
So if you do not know what do I mean by partition of a number, then here it is:
A partition of a positive integer n is, a way of writing n as a sum of positive integers. Two sums that differ only in the order of their summands are considered to be the same partition (For example 1+2+3 and 1+3+2 are same). If order matters then the sum becomes a composition.
Partition(4) = 5
4
3 + 1
2 + 2
2 + 1 + 1
1 + 1 + 1 + 1
Then we have another related term Restricted Partition which is partition having some constraints. For example partition having only odd numbers, partition having only 1 and 2 etc.
In number theory, the partition function p(n) represents the number of possible partitions of a natural number n, which is the number of distinct ways of representing n as a sum of natural numbers.

The right side term on expansion becomes:
(1 + x + x2 + x3 + ...)(1 + x2 + x4 + x6 + ...)(1 + x3 + x6 + x9 + ...) ....
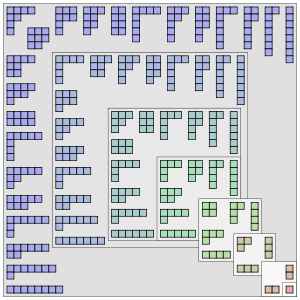
Partitions can also be visualized by Young diagrams or Ferrous diagrams.
Young Diagram makes use of boxes and Ferrous Diagrams make use of dots to represent the same information (as shown below).
So the problem is to write an algorithm that will print all the partitions for a number. There is one very good implementation at Princeton university page under the topic of recursion. Here it is reproduced:
Let me know your feedback. Thanks.
So if you do not know what do I mean by partition of a number, then here it is:
A partition of a positive integer n is, a way of writing n as a sum of positive integers. Two sums that differ only in the order of their summands are considered to be the same partition (For example 1+2+3 and 1+3+2 are same). If order matters then the sum becomes a composition.
Partition(4) = 5
4
3 + 1
2 + 2
2 + 1 + 1
1 + 1 + 1 + 1
Then we have another related term Restricted Partition which is partition having some constraints. For example partition having only odd numbers, partition having only 1 and 2 etc.
In number theory, the partition function p(n) represents the number of possible partitions of a natural number n, which is the number of distinct ways of representing n as a sum of natural numbers.

The right side term on expansion becomes:
(1 + x + x2 + x3 + ...)(1 + x2 + x4 + x6 + ...)(1 + x3 + x6 + x9 + ...) ....
Partitions can also be visualized by Young diagrams or Ferrous diagrams.
Young Diagram makes use of boxes and Ferrous Diagrams make use of dots to represent the same information (as shown below).

The partition 6 + 4 + 3 + 1 of the positive number 14 can be represented by:
So the problem is to write an algorithm that will print all the partitions for a number. There is one very good implementation at Princeton university page under the topic of recursion. Here it is reproduced:
public class Partition { public static void partition(int n) { partition(n, n, ""); } public static void partition(int n, int max, String prefix) { if (n == 0) { StdOut.println(prefix); return; } for (int i = Math.min(max, n); i >= 1; i--) { partition(n-i, i, prefix + " " + i); } } public static void main(String[] args) { int N = Integer.parseInt(args[0]); partition(N); } }
% java Partition 4 % java Partition 6
4 6
3 1 5 1
2 2 4 2
2 1 1 4 1 1
1 1 1 1 3 3
3 2 1
3 1 1 1
2 2 2
2 2 1 1
2 1 1 1 1
1 1 1 1 1 1
Let me know your feedback. Thanks.
No comments:
Post a Comment